Day 3: Binary Tree-I

They are everywhere.

What is a Tree?

Trees are non-linear data structures that are quite often used to represent hierarchical data with a set of connected nodes.

Example:

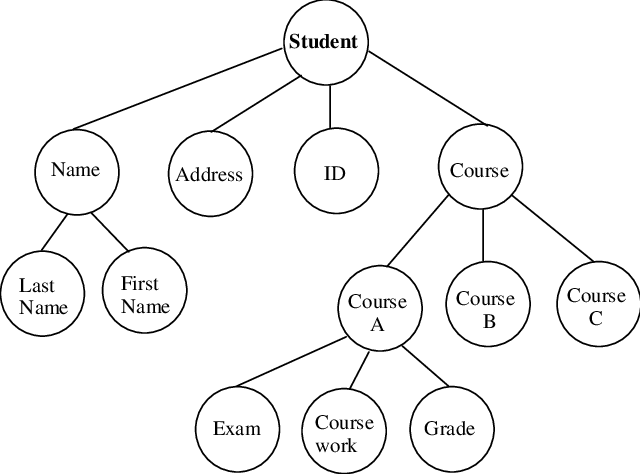
The above example student has a set of hierarchical data such as Name, Address, Course and another set of hierarchical data followed on.

What is a Binary Tree?

A binary tree is a tree data structure made up of nodes, each of which has at most two children, known as the left and right nodes. The tree begins with a single node called the root.

Each node in a binary tree contains

• Data
• Pointer to the left node.
• Pointer to the right node.

Applications of Binary Tree

• Binary Search Tree - Used in many search applications where data is constantly entering/leaving, such as the map and set objects in many languages' libraries.
• Binary Space Partition - Used in almost every 3D video game to determine what objects need to be rendered.
• Binary Tries - Used in almost every high-bandwidth router for storing router-tables.
• Hash Trees - Used in torrents and specialized image signatures in which a hash needs to be verified, but the whole file is not available. Also used in blockchains for eg. Bitcoin.
• Heaps - Used in implementing efficient priority queues, which in turn are used for scheduling processes in many operating systems, Quality-of-Service in routers, and A* (path-finding algorithm used in AI applications, including robotics and video games). Also used in heap-sort.
• Huffman Coding Tree (Chip Uni) - Used in compression algorithms, such as those used by the .jpeg and .mp3 file-formats.
• GGM Trees - Used in cryptographic applications to generate a tree of pseudo-random numbers.
• Syntax Tree - Constructed by compilers and (implicitly) calculators to parse expressions.
• Treap - Randomized data structure used in wireless networking and memory allocation.
• T-tree - Though most databases use some form of B-tree to store data on the drive, databases that keep all (most) their data in memory often use T-trees to do so.

Binary Tree Implementation

We will have a Node class, which has two attributes data, left and right.

Node.java

public class Node {
    int data;
    Node left;
    Node right;

    public Node(int data){
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

Insertion into Binary Tree.

• If the root is null, create a new Node and make it the root.
• If the root already exists, then recursively search for empty locations(left, or right).

• Upon finding an empty left or right child, the new element is inserted. By convention, the insertion always begins from the left child node.

    public void insert(int key)
    {
  
        if (root == null) {
            root = new Node(key);
            return;
        }
        Queue<Node> q = new LinkedList<Node>();
        q.add(root);
  
        while (!q.isEmpty()) {
            root = q.peek();
            q.remove();
  
            if (root.left == null) {
                root.left = new Node(key);
                break;
            }
            else
                q.add(root.left);
  
            if (root.right == null) {
                root.right = new Node(key);
                break;
            }
            else
                q.add(root.right);
        }
    }
  

Searching in Binary Tree.

• If the root is null, then there is nothing to search for, so return False.
• As a binary tree doesn't follow any insertion principles like in Binary Search Trees, we have to do a complete traversal to search a node in Binary Tree.

    public boolean Search(Node root, int value){
        if(root==null){
            return false;
        }

        if(root.data == value){
            return true;
        }

        //Left Sub Tree
        boolean LST = Search(root.left, value);

        //Right Sub Tree
        boolean RST = Search(root.right, value);

        return LST || RST;
    }

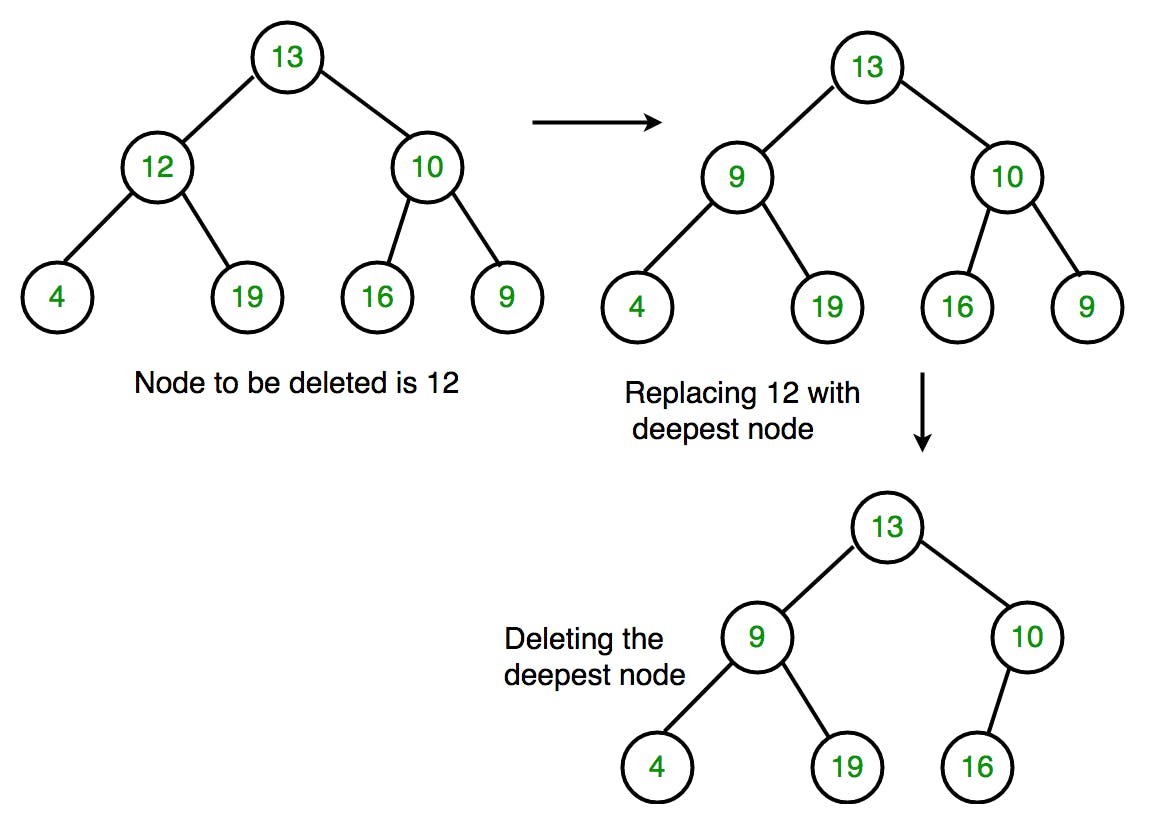
Deletion in Binary Tree.

• Starting at the root, find the deepest and rightmost node in the binary tree and the node which we want to delete.
• Replace the deepest rightmost node’s data with the node to be deleted.
• Then delete the deepest rightmost node.

//Code taken from GFG
public void deleteDeepest(Node root, Node delNode)
    {
        Queue<Node> q = new LinkedList<Node>();
        q.add(root);

        Node temp = null;

        // Do level order traversal until last node
        while (!q.isEmpty())
        {
            temp = q.peek();
            q.remove();

            if (temp == delNode)
            {
                temp = null;
                return;

            }
            if (temp.right!=null)
            {
                if (temp.right == delNode)
                {
                    temp.right = null;
                    return;
            }
            else
                q.add(temp.right);
        }

        if (temp.left != null)
        {
            if (temp.left == delNode)
            {
                temp.left = null;
                return;
            }
            else
                q.add(temp.left);
        }
    }

//Finding the node to be deleted and the leaf node.
public void delete(Node root, int key)
{
    if (root == null)
        return;

    if (root.left == null &&
       root.right == null)
    {
        if (root.data == key)
        {
              root=null;
              return;
        }
        else
            return;
    }

    Queue<Node> q = new LinkedList<Node>();
    q.add(root);
    Node temp = null, keyNode = null;

    // Do level order traversal until
    // we find key and last node.
    while (!q.isEmpty())
    {
        temp = q.peek();
        q.remove();

        if (temp.data == key)
            keyNode = temp;

        if (temp.left != null)
            q.add(temp.left);

        if (temp.right != null)
            q.add(temp.right);
    }

    if (keyNode != null)
    {
        int x = temp.data;
        deleteDeepest(root, temp);
        keyNode.data = x;
    }
}

Traversals on Binary Tree.

Another frequently used tree operation is traversal. Tree traversal is the process of visiting each node present in a tree. There are three methods of tree traversal:

• In-order traversal
• Post-order traversal
• Pre-order traversal

In-Order Traversal

In this traversal method, the left subtree is visited first, then the root, and later the right sub-tree. We should always remember that every node may represent a subtree itself.

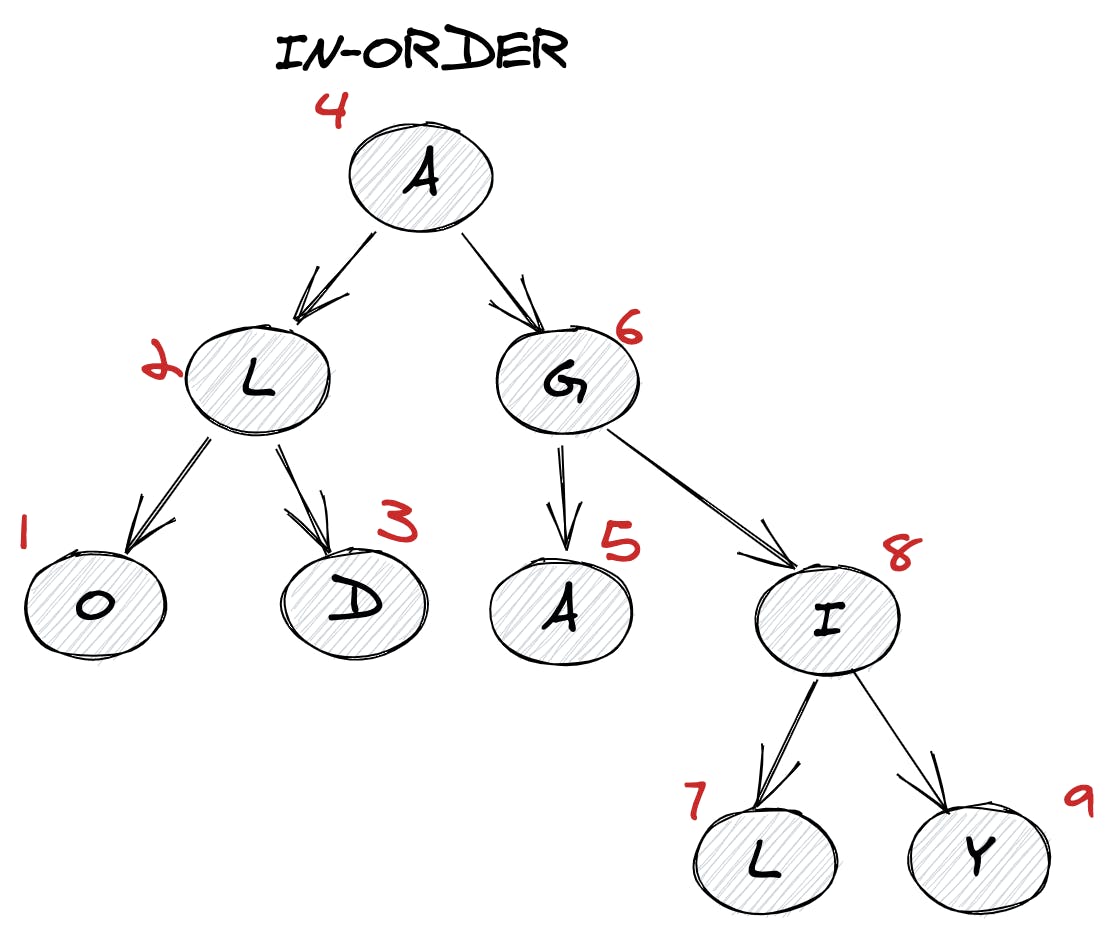
• Recursively traverse Left Subtree.
• Visit the root node.
• Recursively traverse Right Subtree.

Inorder Traversal using recursion.

    /**
     * inOrder Traversal Using Recursion
     * @param node
     * @return
     */
    public List<Integer> inOrderTraversalsUsingRecursion(Node node){
        List<Integer> result = new ArrayList<Integer>();

        //Edge case
        if(node==null) return result;

        inOrderHelper(node, result);

        return result;
    }

    private void inOrderHelper(Node node, List<Integer> result) {

        //Edge Case
        if(node==null) return;

        //Left sub tree
        inOrderHelper(node.left, result);

        //Adding into List
        result.add(node.value);

        //Right Sub Tree
        inOrderHelper(node.right, result);
    }

In-Order Traversal using stack

    public static void inorderIterative(Node root)
    {
        // create an empty stack
        Stack<Node> stack = new Stack<>();

        // start from the root node (set current node to the root node)
        Node curr = root;

        // if the current node is null and the stack is also empty, we are done
        while (!stack.empty() || curr != null)
        {
            // if the current node exists, push it into the stack (defer it)
            // and move to its left child
            if (curr != null)
            {
                stack.push(curr);
                curr = curr.left;
            }
            else {
                // otherwise, if the current node is null, pop an element from
                // the stack, print it, and finally set the current node to its
                // right child
                curr = stack.pop();
                System.out.print(curr.data + " ");

                curr = curr.right;
            }
        }

Pre-Order Traversal

In preorder traversal, first, the root node is visited, then the left sub-tree, and after that right sub-tree is visited.

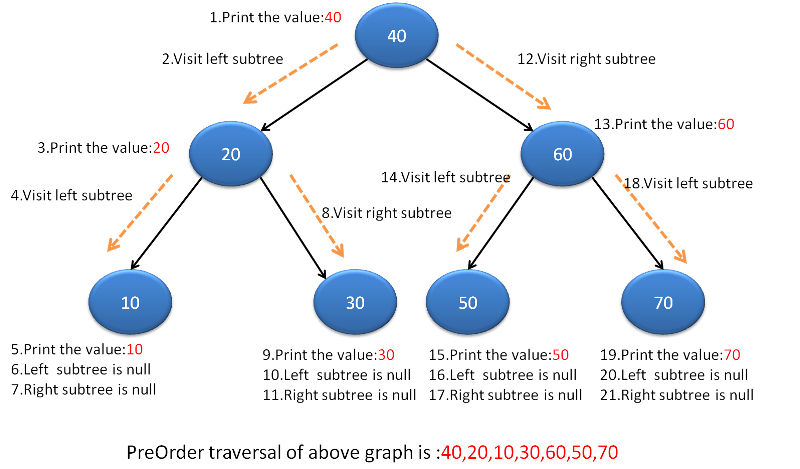
• Visit the root node.
• Recursively traverse Left Subtree.
• Recursively traverse Right Subtree.

Pre-Order Traversal using recursion.

    /**
     * inOrder Traversal Using Recursion
     * @param node
     * @return
     */
    public List<Integer> preOrderTraversalsUsingRecursion(Node node){
        List<Integer> result = new ArrayList<Integer>();

        //Edge case
        if(node==null) return result;

        preOrderHelper(node, result);

        return result;
    }

    private void preOrderHelper(Node node, List<Integer> result) {

        //Edge Case
        if(node==null) return;

        //Adding into List
        result.add(node.value);

        //Left sub tree
        preOrderHelper(node.left, result);

        //Right Sub Tree
        preOrderHelper(node.right, result);
    }

Pre-Order Traversal using stack.

    public static void preorderIterative(Node root)
    {
        // return if the tree is empty
        if (root == null) {
            return;
        }

        // create an empty stack and push the root node
        Stack<Node> stack = new Stack<>();
        stack.push(root);

        // loop till stack is empty
        while (!stack.empty())
        {
            // pop a node from the stack and print it
            Node curr = stack.pop();

            System.out.print(curr.data + " ");

            // push the right child of the popped node into the stack
            if (curr.right != null) {
                stack.push(curr.right);
            }

            // push the left child of the popped node into the stack
            if (curr.left != null) {
                stack.push(curr.left);
            }

            // the right child must be pushed first so that the left child
            // is processed first (LIFO order)
        }

Post-Order Traversal

In this traversal method, the root node is visited last, hence the name. First, we traverse the left subtree, then the right subtree, and finally the root node.

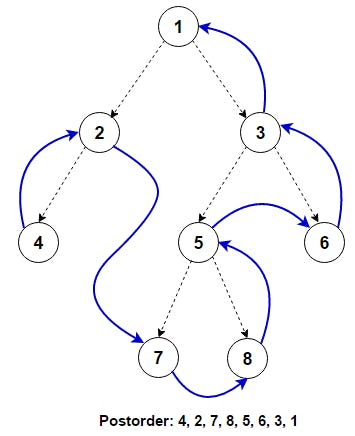
• Recursively traverse Left Subtree.
• Recursively traverse Right Subtree.
• Visit the root node.

Post-Order Traversal using recursion.

    public List<Integer> postOrderTraversalUsingRecursionn(Node node){
        //Edge Case
        if(node==null) return new ArrayList<Integer>();

        List<Integer> result = new ArrayList<Integer>();

        postOrderHelper(node, result);

        return result;
    }

    private void postOrderHelper(Node node, List<Integer> result) {
        //Base Case
        if(node==null) return;

        //Left Sub Tree
        postOrderHelper(node.left, result);

        //Right Sub Tree
        postOrderHelper(node.right, result);

        //Adding to  List
        result.add(node.value);
    }

Post-Order Traversal using stack.

public List<Integer> postOrderTraversal(Node node, List<Integer> result)
{
    ArrayList<Integer> postOrderIterative(Node node)
    {
        Stack<Node> S = new Stack<Node>();

        // Check for empty tree
        if (node == null)
            return list;
        S.push(node);
        Node prev = null;
        while (!S.isEmpty()) {
            Node current = S.peek();

            /* go down the tree in search of a leaf an if so
            process it and pop stack otherwise move down */
            if (prev == null || prev.left == current || prev.right == current) {
                if (current.left != null)
                    S.push(current.left);
                else if (current.right != null)
                    S.push(current.right);
                else {
                    S.pop();
                    list.add(current.data);
                }

                /* go up the tree from left node, if the
                child is right push it onto stack otherwise
                process parent and pop stack */
            }
            else if (current.left == prev) {
                if (current.right != null)
                    S.push(current.right);
                else {
                    S.pop();
                    list.add(current.data);
                }

                /* go up the tree from right node and after
                coming back from right node process parent
                and pop stack */
            }
            else if (current.right == prev) {
                S.pop();
                list.add(current.data);
            }

            prev = current;
        }

        return list;
    }
}

Types of Binary Tree

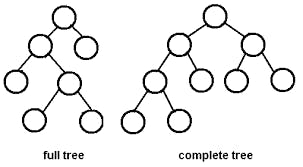
• Full Binary Tree

  A full Binary tree is a special type of binary tree in which every parent node/internal node has either two or no children.

• Perfect Binary Tree

  A perfect binary tree is a type of binary tree in which every internal node has exactly two child nodes and all the leaf nodes are at the same level.

• Complete Binary Tree

  A complete binary tree is just like a full binary tree, but with two major differences like Every level must be completely filled. All the leaf elements must lean towards the left. The last leaf element might not have a right sibling i.e. a complete binary tree doesn't have to be a full binary tree.